서로소 집합
먼저 중학생 때 배웠던 서로소를 떠올려보자. 어떤 두 수 A와 B가 있을 때, 두 수의 공약수가 1을 제외하고는 존재하지 않는 수를 서로소라고 부른다. 이를 고등학생 때 배운 집합의 개념을 빌려 그림으로 표현해 보자.
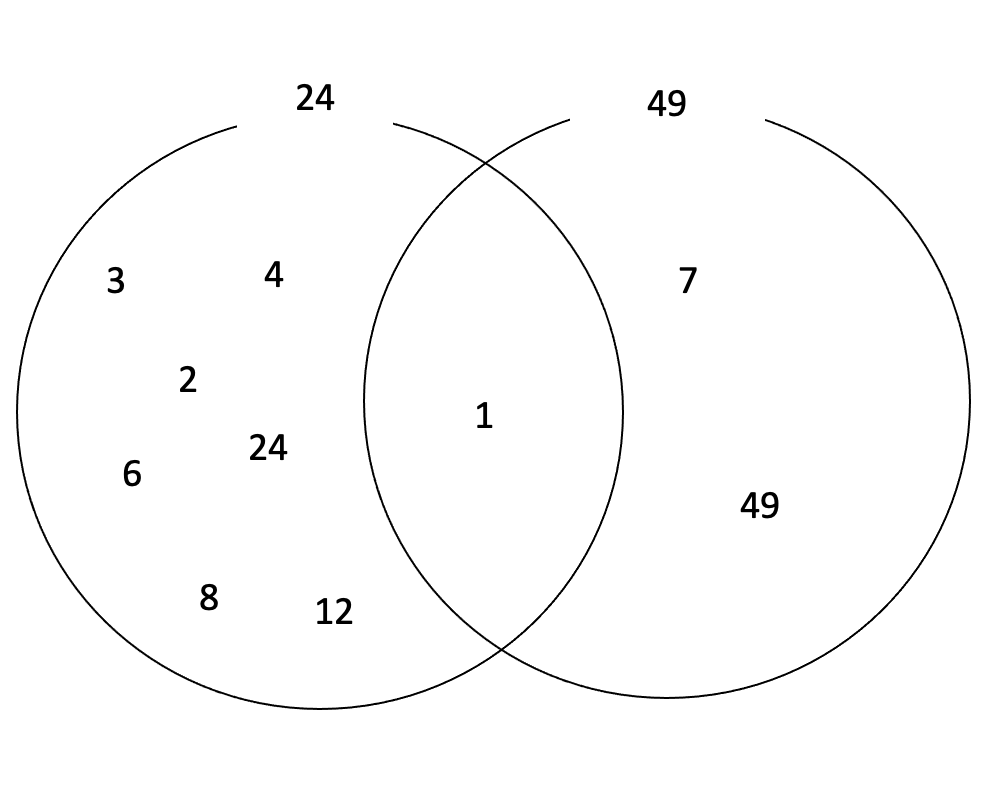
위의 그림은 24와 49의 약수를 벤다이어그램으로 표현한 것이다. 그림을 보면 둘의 공약수가 오직 1만 존재하는 것을 볼 수 있으며, 이런 형태의 수를 서로소라고 부른다.
이제 집합에서의 서로소가 무엇을 의미하는지 알아보자. 정수에서 서로소는 서로의 약수가 1을 제외하고 겹치지 않는 것을 의미했다. 이와 유사하게 서로소 집합은 두 집합의 원소가 겹치지 않는 것을 의미한다. 예를 들면 아래의 그림과 같은 집합을 서로소 집합이라 부를 수 있다.

위의 두 집합 A와 B를 보면, 두 집합이 포함하고 있는 원소가 겹치지 않는 것을 볼 수 있다. 이러한 집합을 서로소 집합이라 부르며, 이를 다시 그래프로 나타내면 다음과 같이 표현할 수 있다.
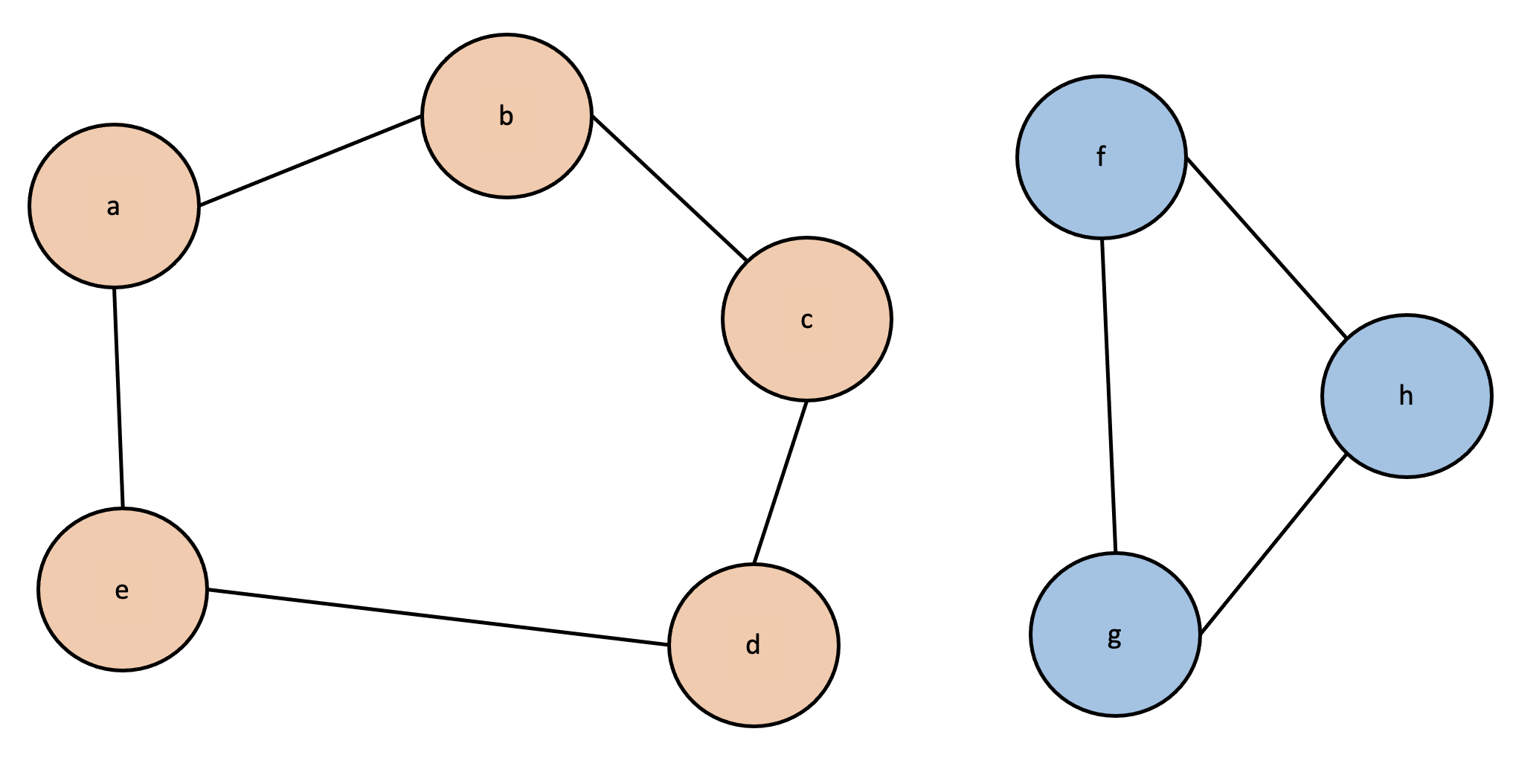
위의 그림처럼 서로 연결되어 있는 노드들을 같은 집합으로 묶고 색깔을 칠해준다고 했을 때, 색깔이 다른 노드는 인접해있지 않으며 서로 다른 집합에 속한다고 표현할 수 있다. 오늘 알아볼 서로소 집합 알고리즘은 노드들과 간선의 정보가 주어졌을 때, 간선을 통해 이동할 수 있는 노드들을 한 집합으로 묶어주는 알고리즘이다.
Union-Find Algorithm
서로소 집합 알고리즘은 다음의 두 가지 연산으로 이루어진다.
- find_parent : 현재 노드의 최상단 부모 노드를 찾는 연산
- union_parent : 간선 정보가 주어졌을 때, 간선으로 이어진 두 노드의 집합을 합쳐주는 연산(합집합 연산)
두 연산의 과정을 그림과 함께 살펴보자!

먼저 기본적으로 간선 정보가 주어지지 않은 초기 상황에는 parent 배열의 값이 각각 자기 자신으로 설정이 되어있다. 이제 간선 정보가 하나씩 들어오면서 각 노드의 부모 정보가 바뀔 것이다.
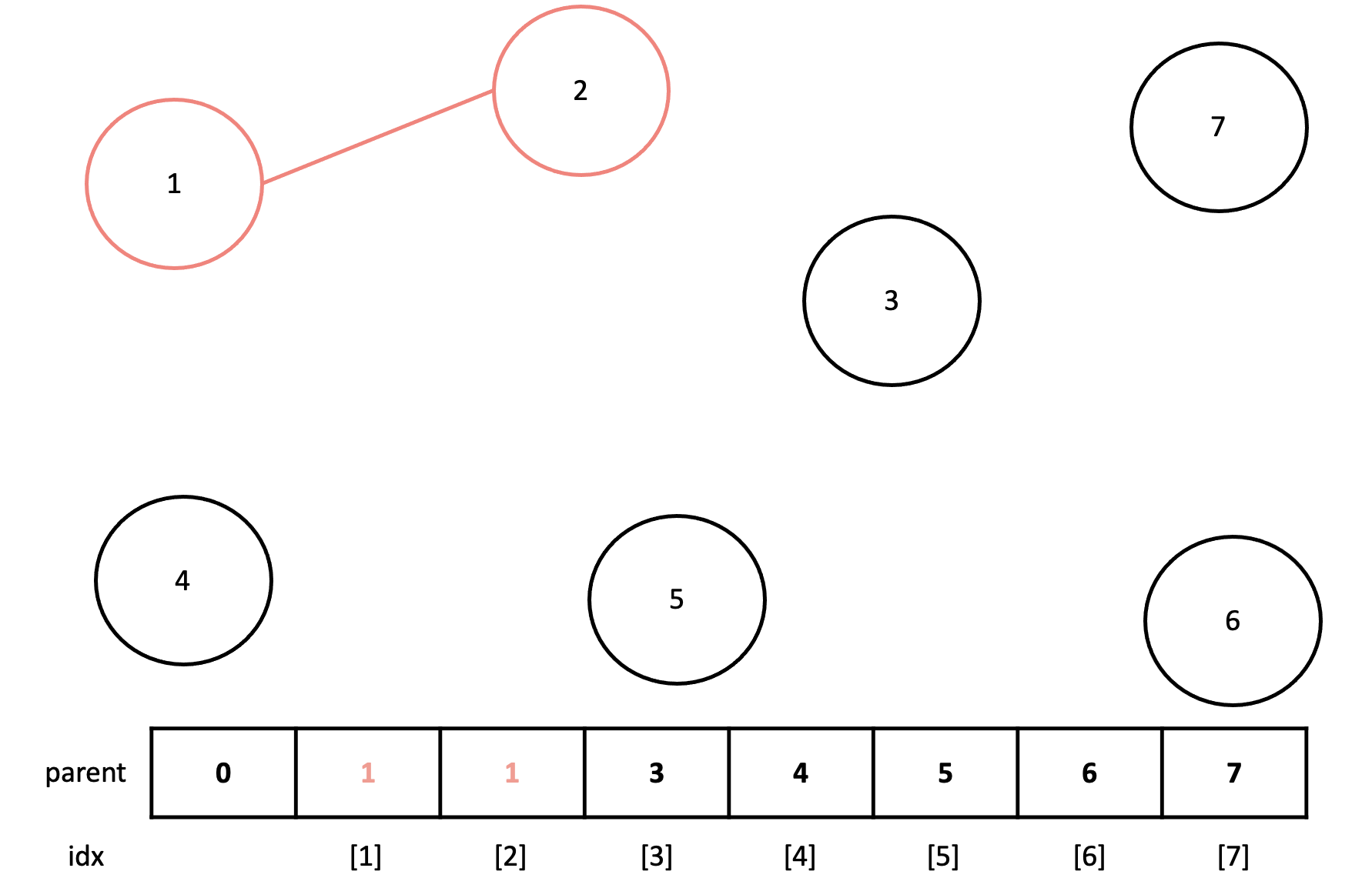
그림과 같이 1과 2를 연결하는 간선이 입력으로 들어왔다고 생각해보자. 현재 1번 노드의 부모는 자기 자신인 1이고, 2번 노드 또한 마찬가지로 부모가 자기 자신이다. 간선이 주어졌으므로 두 노드의 부모를 합쳐주어야 하는데, 부모를 합칠 때에는 부모가 더 작은 값으로 합쳐준다. 따라서 그림에서는 2번 노드의 부모가 1번 노드로 바뀌게 된다.

다음으로 4와 5를 연결하는 간선을 처리할 때의 모습이다.

이번에는 2와 5를 연결하는 간선이 주어진 상황인데, 2번 노드와 5번 노드의 부모는 각각 1번과 4번이다. 이때 parent 배열에서 2번 노드의 부모와 5번 노드의 부모를 바로 바꿔주지 않고, 2번 노드와 5번 노드의 최상위 부모로 먼저 올라간다.
최상위 부모 노드의 조건
최상위 부모 노드는 parent 배열에서의 인덱스 값과 그 위치에 있는 parent 값이 같아야한다! (더 이상 올라갈 부모가 없어야 함)
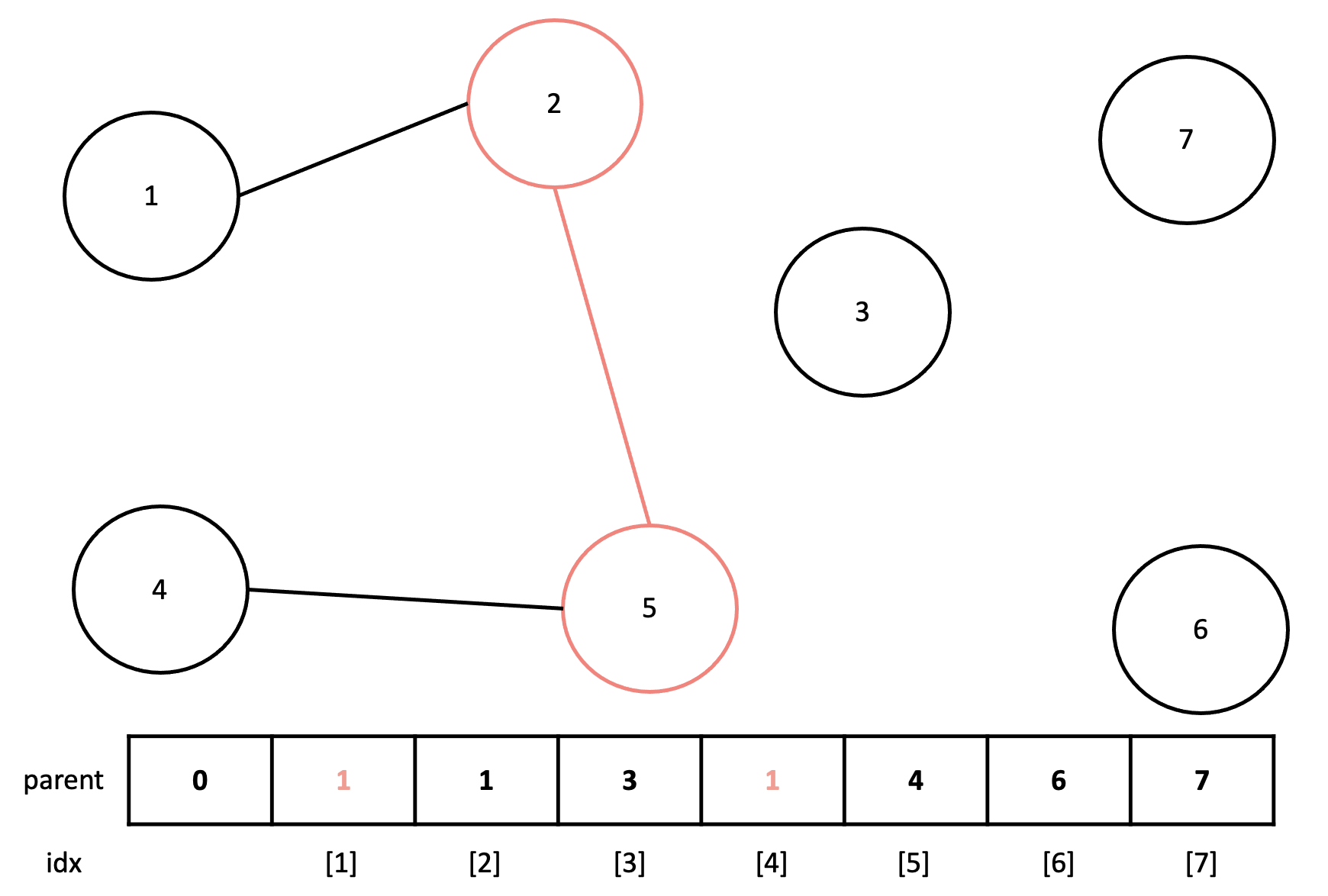
최상위 부모인 1번 노드와 4번 노드를 비교하여 부모의 값이 더 작은 노드로 부모를 바꿔준다. 이렇게 되면 5번 노드의 부모는 여전히 4번이지만, 후에 5번 노드의 최상위 부모를 찾을 때 배열에 있는 값인 4에서 끝나는 것이 아니라 4번 노드의 부모인 1번 노드까지 올라가게 된다. 따라서 5번 노드의 최상위 부모인 1번을 찾을 수 있게 된다.

조금 더 진행을 해서 오른쪽 노드들에 대한 간선도 추가가 되어 6번 노드와 7번 노드의 부모가 3번 노드로 설정된 상황이다. 이후 5번과 6번 노드를 연결하는 간선 정보가 주어졌을 때를 생각해 보자. 먼저 parent[5]와 idx인 5가 서로 다르기 때문에 5번 노드는 최종 부모 노드가 아님을 알 수 있다. 따라서 parent[5]인 4번 노드로 이동하게 된다.

이때 parent[4] 또한 4가 아니므로 최종 부모 노드가 아니다. 따라서 4의 부모인 1번 노드로 이동하게 된다.

마지막으로 1번 노드는 부모가 자기 자신이므로, 최종 부모 노드임을 알 수 있다. 이제 다시 이전 노드인 4번 노드로 돌아가 최종 부모의 정보를 업데이트해준다.

마지막으로 다시 5번 노드로 돌아오면, 최종 부모인 1번 노드로 부모 정보를 업데이트 해준다. 이제 6번이 속한 집합의 최종 부모인 3번과 5번이 속한 집합의 최종 부모인 1번을 비교하여, 부모 노드의 번호가 작은 쪽으로 병합을 진행한다. 따라서 3번 노드의 최종 부모를 1로 바꿔준다.

이렇게 업데이트를 해주면, 이후 6번과 7번 노드의 최종 부모를 찾을 때에도 3번으로 이동하고 나서, 3번의 부모인 1번으로 이동하여 결국 최종 부모인 1번 노드를 찾을 수 있게 된다.
find_parent 함수와 union_parent 함수를 코드로 구현하면 다음과 같다.
def find_parent(parent, x):
# 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
# 두 원소가 속한 집합을 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b'Algorithm' 카테고리의 다른 글
| [Algorithm] 위상 정렬(Topology Sort) (1) | 2023.03.21 |
|---|---|
| [Algorithm] 최단 경로 알고리즘(Shortest Paths) - 다익스트라 (0) | 2023.03.20 |
| [Python] 백준 21606번 아침 산책 (1) | 2023.03.18 |
| [Algorithm] BFS & DFS (1) | 2023.03.17 |
| [Python] 백준 2261 가장 가까운 두 점 (4) | 2023.03.14 |
