https://www.acmicpc.net/problem/21606
21606번: 아침 산책
1번 정점에서 시작하고 3, 4번 정점에서 끝나는 경로, 3번 정점에서 시작하고 1, 4번 정점에서 끝나는 경로, 4번 정점에서 시작하고 1, 3, 5번 정점에서 끝나는 경로, 5번 정점에서 시작하고 4번 정점
www.acmicpc.net
이번에 풀 문제는 아침 산책이라는 문제다. 이전 문제들과는 달리 서브태스크가 있고 각 태스크마다 배점이 부여되어 있는데, 이를 통해 내 풀이가 어떤 조건을 만족하지 못하는지 알 수 있다. 일단 본격적으로 풀이를 하기에 앞서 문제 요구사항을 짚고 넘어가자!
문제에서 장소를 노드로 표현하였으며, 실내인 노드는 1, 실외인 노드는 0으로 표현하였다.
문제에서 구하고자 하는 것은 실내에서 실내까지의 총경로의 수이며, 중간에 실외가 포함되어도 조건을 충족한다. 단, 실내에서 실내까지 가는 경로에 다른 실내인 장소가 있어서는 안 된다.
장소의 개수는 총 N개이며, N의 범위는 $2 \leq N \leq 2 x 10^5$ 이다.
처음에 문제를 풀 때는 모든 실내에 대해서 실내로 연결되는 지점들을 찾아 카운트를 증가시키는 방식으로 풀이를 진행했다. 이 경우 시간 초과가 발생해 5번 서브태스크에서 점수를 받지 못한다.
비록 시간 초과가 발생하긴 하지만 그래도 답은 찾을 수 있으니 조금만 더 자세히 살펴보고 넘어가자..!
문제의 기본적인 풀이 방식은 다음과 같다.
- 실내인 장소를 찾는다.
- 실내인 장소를 찾으면 그 장소와 연결된 장소를 탐색한다.
- 연결된 장소가 실내이면 현재 장소와 연결된 장소에 경로를 +1 해준다.
- 만약 연결된 장소가 실외이면 실외인 장소로 이동한다.
- 실외인 장소와 연결된 장소 중 실내인 장소를 찾고, 연결된 실내 장소만큼 경로를 증가시킨다. 이때 연결된 실내 장소 또한 경로에 +1을 해준다.
- 연결된 장소가 또 실외인 경우 다시 연결된 장소로 이동해 위의 과정을 반복한다.

이제 그림과 함께 살펴보자! 먼저 1번 장소가 실내이기 때문에 주변 장소들을 탐색한다. 1번과 연결된 2번 장소가 실외이기 때문에 장소를 2번으로 옮겨 검사를 진행한다. 이때 1번 장소를 다시 검사하지 않도록 1번 장소는 방문 처리를 해준다.

2번과 연결된 장소 중 아직 방문하지 않았고, 실내인 장소를 찾아 경로의 개수를 그림과 같이 증가시켜 준다. 이후 실외인 6번 장소로 이동한다. 이때도 마찬가지로 2번 장소를 다시 방문하는 일이 없게끔 2번 장소에 방문 처리를 해준다.
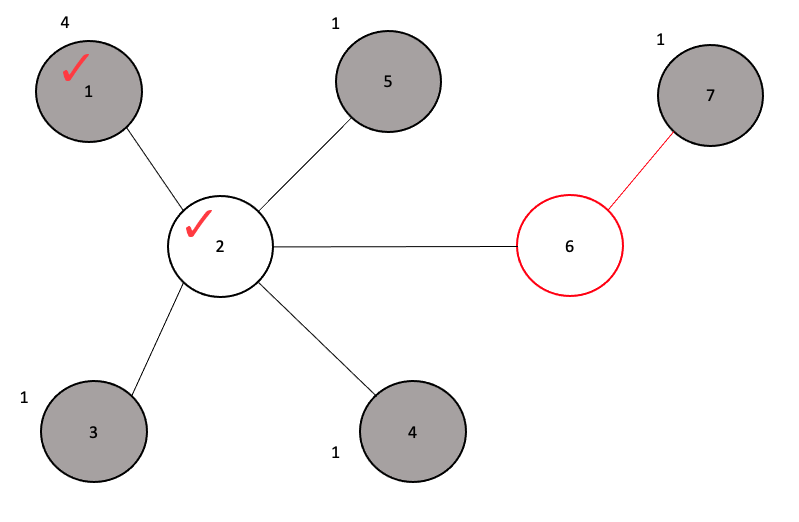
6번 장소에서 연결된 장소 중 실내인 장소가 7번 하나이기 때문에, 1번 장소의 경로를 1 추가시키고 7번 장소 또한 경로를 1 추가시킨다.

이제 함수가 끝날 때에는 실외인 장소들의 방문 표시를 모두 초기화시키는데, 이는 다음 장소를 검사할 때에도 쓰일 수 있게 하기 위함이다.
하지만 처음에 시작점인 1번은 방문 표시를 초기화시키지 않는데, 이는 1번 장소와 연결된 장소들을 검사할 때 연결된 장소들 또한 1번 장소로 가는 경로를 추가시켰기 때문에 다음에 중복으로 세지 않게 하기 위함이다.
위와 같은 과정을 다른 장소들에 대해서 반복해 주면 된다.
이 풀이를 코드로 구현해 보면 다음과 같다.
import sys
sys.setrecursionlimit(10**5)
input = sys.stdin.readline
n = int(input())
A = input().rstrip()
graph = [[] for _ in range(n+1)]
place = [0] * (n+1)
visited = [0] * (n+1)
result = [0] * (n+1)
for i in range(len(A)):
if A[i] == '1':
place[i+1] = 1
for _ in range(n-1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
def dfs(node, start):
if place[node] == 1:
result[node] += 1
result[start] += 1
return
for next_node in graph[node]:
if not visited[next_node]:
visited[next_node] = 1
dfs(next_node, start)
visited[next_node] = 0
ans = 0
for i in range(1, n+1):
if place[i] == 1:
visited[i] = 1
for next_node in graph[i]:
if place[next_node] == 1:
if not visited[next_node]:
result[next_node] += 1
result[i] += 1
else:
visited[next_node] = 1
dfs(next_node, i)
visited[next_node] = 0
print(sum(result))
이제 이러한 풀이가 시간 초과가 발생하는 이유에 대해 생각해 보자. 위에서 언급했다시피 N의 최댓값이 무려 20만이다. 만약 단 하나의 장소가 실외이고, 나머지 모든 실내가 실외인 장소와 연결되어 있다고 생각해보자. 그림으로 나타내면 다음과 같다.
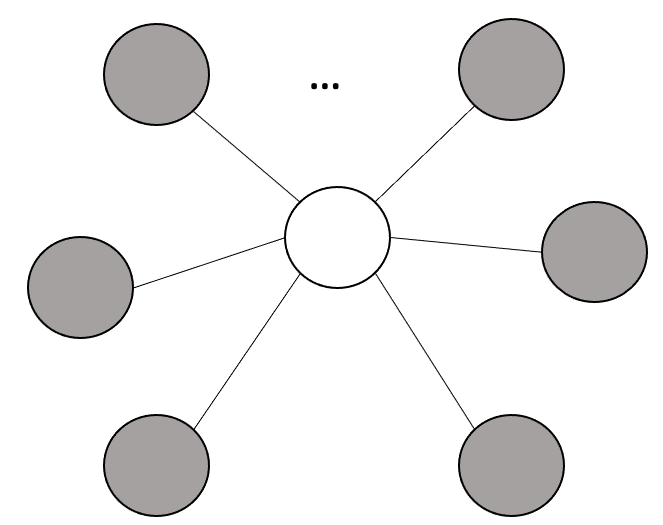
위와 같은 상황에서 언급한 풀이를 적용해 보면, 하나의 실내인 장소에 대해 연결된 모든 실내를 탐색하려면 N-2(현재 장소와 실외 장소를 제외한 실내의 개수) 만큼의 연산이 소요될 것이다. 이러한 연산을 모든 실내인 장소에 대해 진행해야 하므로 총 연산량은 (N-1) x (N-2)가 될 것이고, 빅오 표기법으로 나타내면 $O(n^2)$의 시간이 소요될 것이다. N의 최댓값이 20만이라는 점을 감안했을 때, 이 풀이법은 시간 초과를 피하지 못할 것이다.
따라서 이 문제에서 만점을 받기 위해서는 다른 풀이를 생각해내야 한다.
위의 그림에 대해 다시 생각해 보자. 현재 실외인 장소가 단 하나이고, 모든 실내인 장소는 이 실외인 장소를 통해 다른 모든 실내로 이동할 수 있다. 즉, 실외인 장소와 연결되어 있는 실내인 장소는 총 N-1 개이고, 이 N-1 개의 장소들은 서로 이동이 가능한 것이다.
이를 통해 한 가지 유추할 수 있는 사실이 있는데, 일단 이름이 너무 헷갈리니 실외인 장소를 A라고 해두자. 만약 A와 연결된 실내 장소의 개수가 B개 일 때, A를 통해 이동할 수 있는 경로의 총가짓수는 B개 중 두 개를 선택하는 경우의 수와 같을 것임을 알 수 있다. 단, 1 -> 2가 가능하다면 2 -> 1 또한 다른 경로로 생각하기 때문에, 단순히 B개 중 두 개를 선택하는 조합이 아니라 두 개를 선택한 뒤 순서를 배치하는 순열로 생각을 해주어야 한다. 이에 따라 총경로의 수는 (N-1) x (N-2) 가 된다.
따라서 실외 장소와 연결된 실내 장소의 개수를 세어주면 총 경로의 수도 손쉽게 구할 수 있다!
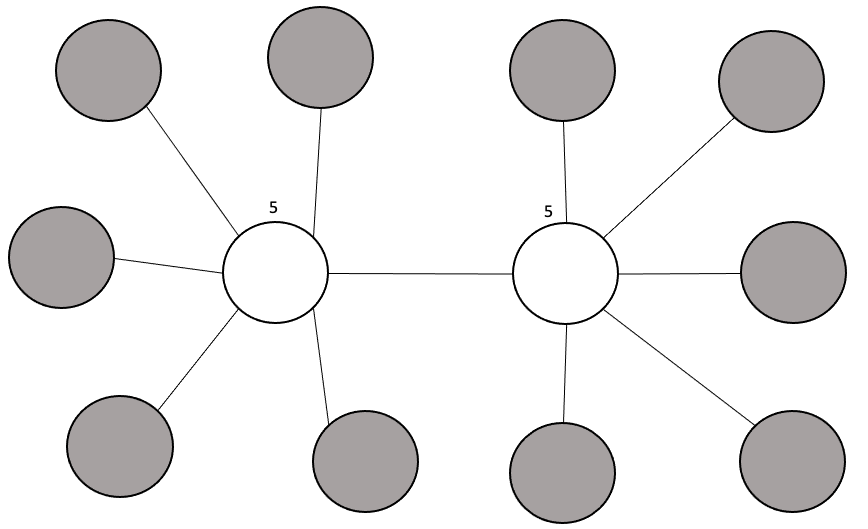
위의 그림과 같은 경우는 어떨까? 실외인 장소가 여러 개가 이어져있는데, 문제에서 주어진 경로가 트리의 형태를 따르므로 단순히 두 실외 장소와 연결된 실내 장소의 개수를 더해주면 된다! 즉, 두 개의 실외 장소를 하나의 실외 장소로 봐도 다르지 않다는 뜻이다. 따라서 우리는 장소가 실외이면 그 장소와 연결된 실내 장소의 개수를 세어주고, 만약에 또 다른 실외 장소와 연결이 되어있다면, 연결된 실외 장소로 이동하여 그 장소와 연결된 실내 장소를 다시 세어준다. 그 뒤에 모든 실내 장소의 개수를 더하여 그 값으로 답을 구하는 것이다.
위의 그림에서 두 실외 장소와 연결되어 있는 실내 장소의 개수가 모두 5개 이므로, 총 경로의 수는 10 x 9 = 90 가지가 나올 것이다. 하지만 풀이가 여기서 끝난다면 아래의 그림과 같은 상황에서는 경로의 수를 정확하게 파악하지 못한다.
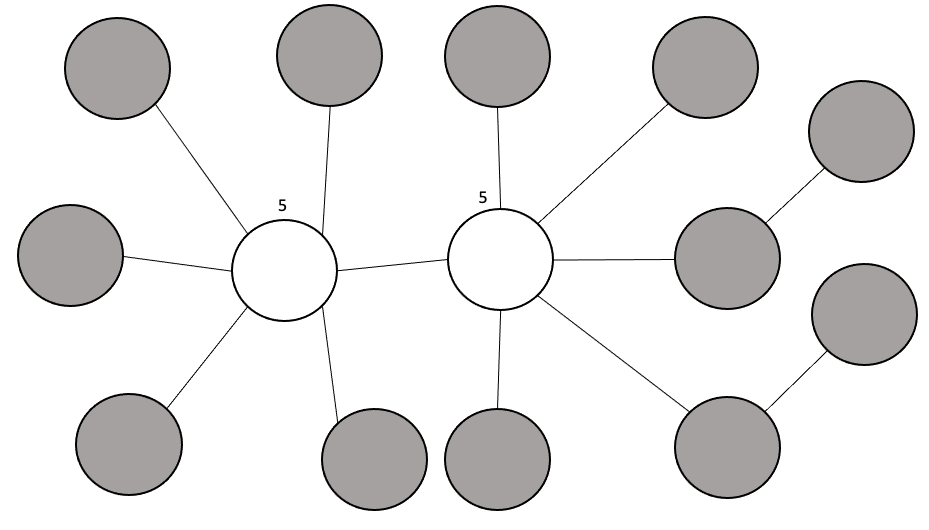
검사를 장소가 실외인 경우만 해주기 때문에 실외와 연결되어 있지는 않지만 바로 연결된 실내 장소는 카운트해주지 못한다. 이를 방지하기 위해 현재 검사하는 장소가 실내인 경우 바로 연결되어 있는 실내의 장소만 세어주어 경로를 추가해 주는 처리를 해주었다. 지금까지의 풀이를 코드로 구현해 보면 다음과 같다.
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
n = int(input())
A = input().rstrip()
graph = [[] for _ in range(n+1)]
place = [0] * (n+1)
visited = [0] * (n+1)
for i in range(len(A)):
if A[i] == '1':
place[i+1] = 1
for _ in range(n-1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
def dfs(node):
res = 0
for next_node in graph[node]:
if place[next_node] == 0:
if not visited[next_node]:
visited[next_node] = 1
res += dfs(next_node)
else:
res += 1
return res
ans = 0
for i in range(1, n+1):
if place[i] == 0:
if not visited[i]:
visited[i] = 1
res = dfs(i)
ans += res * (res - 1)
else:
for next_node in graph[i]:
if place[next_node] == 1:
ans += 1
print(ans)이 풀이의 경우 모든 간선에 대해 한 번씩의 조사만 하기 때문에 선형의 시간복잡도로 문제를 해결할 수 있다.
'Algorithm' 카테고리의 다른 글
| [Algorithm] 최단 경로 알고리즘(Shortest Paths) - 다익스트라 (0) | 2023.03.20 |
|---|---|
| [Algorithm] 서로소 집합(Disjoint Set) 알고리즘 (1) | 2023.03.19 |
| [Algorithm] BFS & DFS (1) | 2023.03.17 |
| [Python] 백준 2261 가장 가까운 두 점 (4) | 2023.03.14 |
| [Python] 백준 13334번 철로 (2) | 2023.03.14 |
