이분 매칭 알고리즘은 유량 그래프의 특수한 형태이다. 유량 그래프는 다음 포스팅에서 다루기로 하고... 이분 매칭 알고리즘에 대해 알아보자.
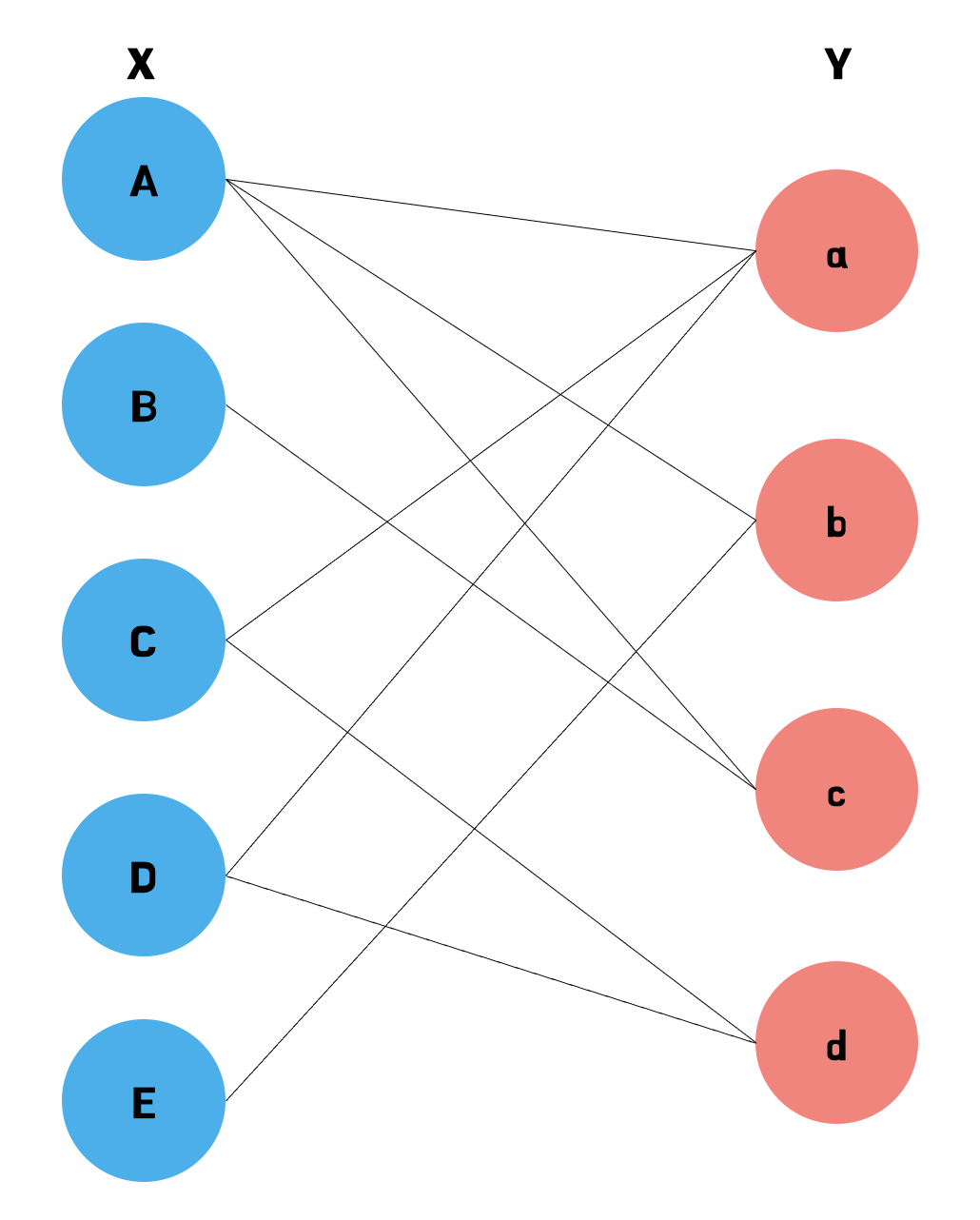
이분 매칭 알고리즘을 알아보기 전에, 이분 그래프에 대해 먼저 알고 넘어가야 한다. 이분 그래프란 정점을 두 개의 그룹으로 나누었을 때, 모든 간선의 양 끝 정점이 서로 다른 그룹에 속하는 형태의 그래프를 말한다. 위의 그림에서 보면 파란색 노드의 집합을 X, 빨간색 노드의 집합을 Y로 표현할 수 있고, 따라서 위의 그래프는 이분 그래프이다.
이분 매칭 알고리즘은 위와 같은 이분 그래프에서 최대 매칭의 개수를 찾는 것과 같다. 매칭이란 간선 하나를 선택하는 것을 말하는데, 예를 들어 그림에서 A와 a를 연결하는 간선을 선택하면 (A, a)라는 매칭이 생기는 것이다. 각 노드들은 딱 한 번만 선택이 되어야 하므로, 이 간선을 선택했을 때 A 또는 a와 연결되어 있는 간선은 더 이상 선택이 불가능하다.
이제 이분 매칭 알고리즘의 과정을 살펴보자.
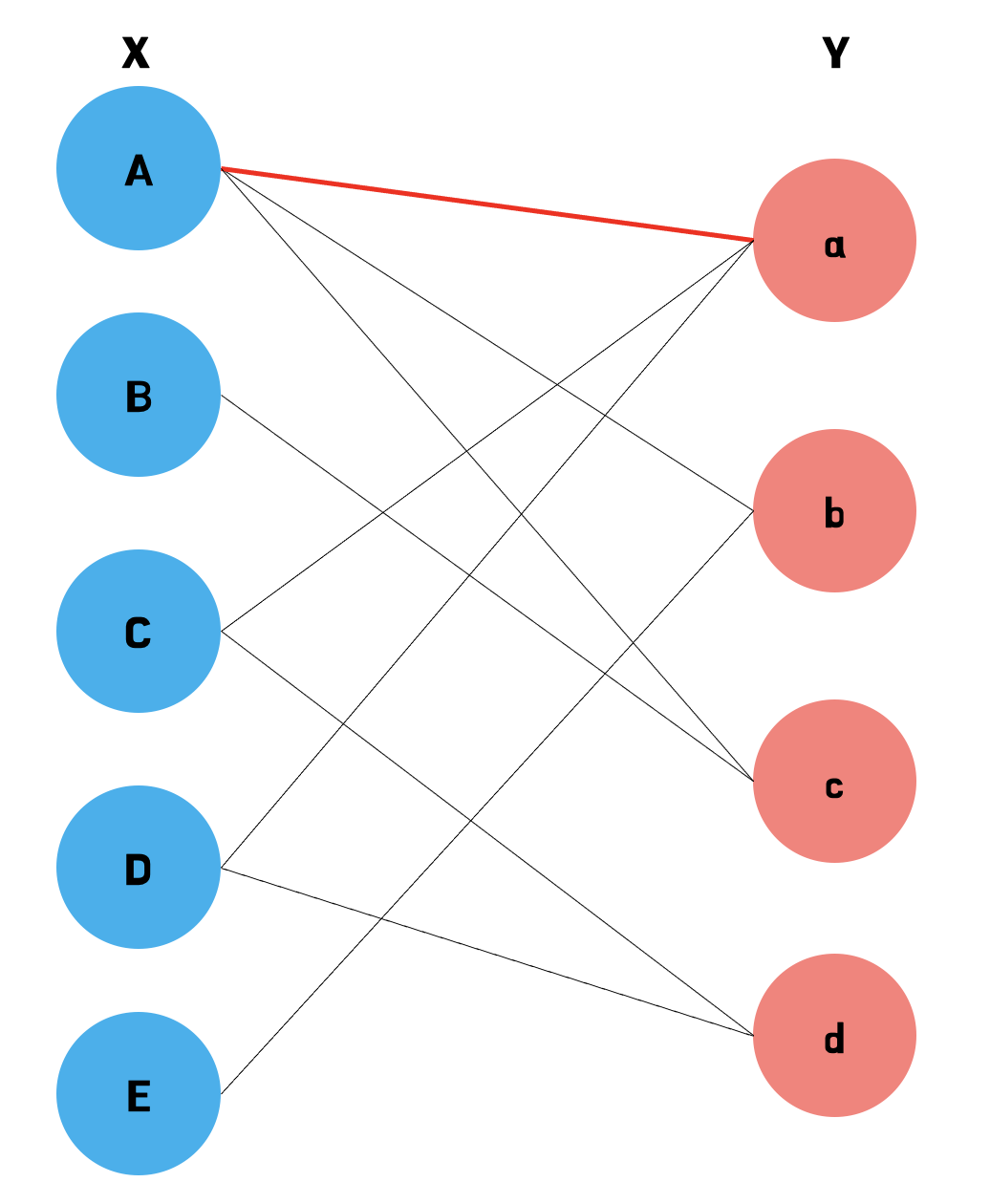
먼저 위의 그림과 같이 (A, a) 매칭을 선택한다.

이후 (B, c) 매칭을 선택한다.

그다음 (C, a) 매칭을 선택하게 되는데, 이때 a는 이미 (A, a) 매칭에 속해있다. 이러한 상황에서는 (C, a) 매칭을 선택하고 원래 있던 (A, a) 매칭을 끊는다.

A는 매칭이 끊어졌기 때문에 아직 남아있는 간선을 추가로 탐색하게 되고, (A, b) 매칭이 선택된다.

이후 (D, a) 매칭이 선택되고, 원래 있던 (C, a) 매칭은 끊기게 된다. 이후 (C, d) 매칭이 새로 선택된다.
마지막 노드 E는 가능한 매칭이 (E, b) 뿐인데, 이 매칭이 선택될 경우 노드 A는 Y의 다른 노드와 매칭이 불가능하기 때문에 노드 E는 매칭이 될 수 없다. 따라서 가능한 최대 매칭은 위의 그림과 같이 네 가지가 선택될 수 있다.
위의 과정을 코드로 나타내면 다음과 같다.
# matched_Y : Y 그룹의 노드와 매칭된 X 노드의 번호
# matched_X : X 그룹의 노드와 매칭된 Y 노드의 번호
def dfs(x):
visited[x] = True
for y in graph[x]:
# y 노드와 매칭된 노드가 없는 경우, x 노드와 매칭
if matched_Y[y] == 0:
matched_Y[y] = x
matched_X[x] = y
return True
# y 노드가 이미 매칭이 되어있는 경우, y 노드와 매칭되어 있는 노드가 다른 노드와 매칭이 가능한지 확인
elif not visited[matched_Y[y]] and dfs(matched_Y[y]):
# 다른 노드와 매칭이 가능한 경우, y 노드와 x 노드를 매칭
matched_Y[y] = x
matched_X[x] = y
return True
return False
cnt = 0
for i in range(1, n+1):
if matched_X[i] == 0:
visited = [False] * (n+1)
if dfs(i):
cnt += 1
이분 매칭 알고리즘 문제로 풀어볼 만한 것들은 아래와 같다.
https://www.acmicpc.net/problem/11375
11375번: 열혈강호
강호네 회사에는 직원이 N명이 있고, 해야할 일이 M개가 있다. 직원은 1번부터 N번까지 번호가 매겨져 있고, 일은 1번부터 M번까지 번호가 매겨져 있다. 각 직원은 한 개의 일만 할 수 있고, 각각
www.acmicpc.net
기본적인 이분 매칭 알고리즘 문제다. 위의 그림에서 X 그룹과 Y 그룹을 각각 직원과 일로 구분해서 풀 수 있다.
https://www.acmicpc.net/problem/11376
11376번: 열혈강호 2
강호네 회사에는 직원이 N명이 있고, 해야할 일이 M개가 있다. 직원은 1번부터 N번까지 번호가 매겨져 있고, 일은 1번부터 M번까지 번호가 매겨져 있다. 각 직원은 최대 두 개의 일을 할 수 있고,
www.acmicpc.net
이 문제는 위의 열혈강호 문제에 딱 한 가지 조건이 추가되었다. 바로 직원 한 명이 최대 두 개까지의 일을 할 수 있는 것인데, 같은 edge를 가진 직원을 하나씩 더 만든다고 생각하고 풀면 된다.
https://www.acmicpc.net/problem/11377
11377번: 열혈강호 3
첫째 줄에 직원의 수 N과 일의 개수 M, 일을 2개할 수 있는 직원의 수 K가 주어진다. (1 ≤ N, M ≤ 1,000, 1 ≤ K ≤ N) 둘째 줄부터 N개의 줄의 i번째 줄에는 i번 직원이 할 수 있는 일의 개수와 할 수 있
www.acmicpc.net
기본적으로 백준의 열혈강호 시리즈는 다 이분 매칭 문제들인 것 같다. 이 문제는 직원들 중 몇 명만이 일을 두 개씩 할 수 있다는 추가 조건이 붙는다. 이때 k명의 직원을 특정하지는 않기 때문에 k명 이내에서는 어떤 직원이든 일을 두 개씩 할 수 있다.
이 문제는 이분 매칭을 총 두 번 하는 방식으로 풀 수 있다. 이때 두 번째 이분 매칭에서는 매칭이 총 k개 생긴 경우 매칭을 종료해야 한다.
'Algorithm' 카테고리의 다른 글
| [Python] 2020 KAKAO BLIND RECRUITMENT - 블록 이동하기 (0) | 2023.07.15 |
|---|---|
| [Python] 2023 KAKAO BLIND RECRUITMENT - 표 병합 (0) | 2023.07.15 |
| [Python] 2022 KAKAO TECH INTERNSHIP 코딩 테스트 공부 (1) | 2023.07.11 |
| [Algorithm] LCP 배열(Longest Common Prefix Array) (1) | 2023.03.28 |
| [Algorithm] 맨버-마이어스 알고리즘(Suffix Array) (1) | 2023.03.27 |
