접미사 배열이란 특정 문자열에 대한 접미사들을 모두 나열한 뒤, 사전 순으로 정렬을 진행한 배열을 의미한다.
일반적으로 접미사 배열을 만드는 방법은 다음과 같다.
- 문자열에 대해 모든 접미사들을 만들어준다.
- 만들어진 접미사들을 맨 앞글자를 기준으로 정렬한다.
- 이후 정렬 기준을 앞에서 2번째 문자, 3번째 문자 ... 로 늘려가면서 최대 문자열의 길이인 n번째 문자까지 바꿔가며 정렬을 진행한다.
위의 과정을 따르면, 한번 정렬을 진행하는데 $O(n log n)$ 만큼의 시간이 걸리고, 정렬을 최대 문자열의 길이만큼 반복한다고 했으므로 총 시간복잡도는 $O(n^2 log n)$ 과 같이 나타날 것이다.
이를 맨버-마이어스 알고리즘을 통해 $O(n log^2 n)$의 시간복잡도로 단축시킬수 있다. 이제 정렬이 어떤 방식으로 진행되는지 알아보자!
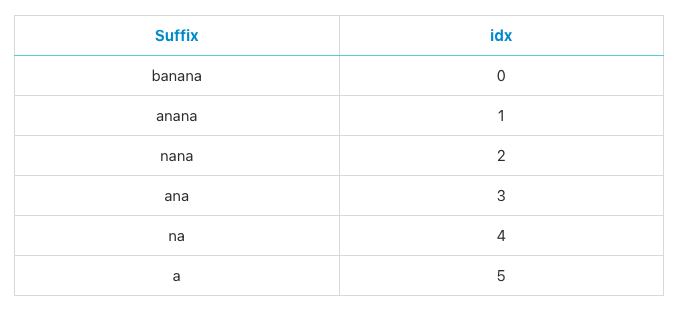
위의 표에서는 banana를 예시로 들었다. banana의 접미사들을 나열하였고, 이를 모두 배열에 담아버리면 메모리 낭비가 심해질 수 있기때문에 실제 배열에는 접미사의 시작 부분이 실제 문자열에서 어느 위치에 존재하는지를 나타내었다.
다음으로 각 접미사들을 비슷한 접미사끼리 같은 그룹으로 묶고, 각 그룹에 rank를 부여하기 위해 다음과 같은 배열을 추가적으로 만들어준다.

위의 표는 각 인덱스에 속하는 접미사의 rank를 나타낸 것이다. rank는 각 접미사의 맨 앞글자를 기준으로 부여하였으며, 문자 'a'의 아스키코드 값과 차이로 계산하였다.
이제 맨 앞글자를 기준으로 정렬을 진행해보자!
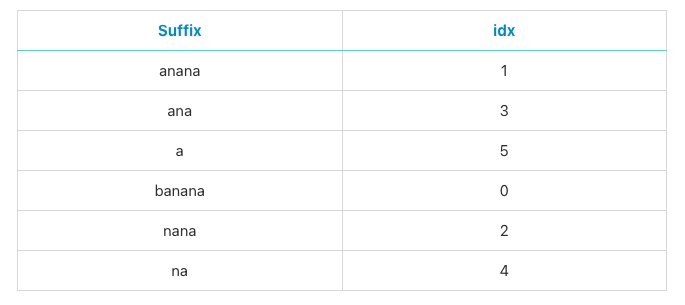
정렬을 한번 진행하면 위와 같은 결과를 얻을수 있다. 이제 첫번째 문자에 대한 비교가 끝났으니 두번째 문자를 비교하는 작업을 진행할 것이다. 그전에 위에서 정의해준 rank 배열을 새로 갱신해야한다. 기존의 rank 배열은 각 접미사의 첫번째 문자를 기준으로 두었으니, 이번에는 두번째 문자를 기준으로 rank 배열을 초기화시킨다.

위의 표를 그룹을 기준으로 나타내자면 다음과 같다.

첫 정렬 이후 그룹이 위와 같이 나누어져있을때, 이를 한번 더 세분화시켜 아래와 같이 만든것이다.

이때 원래의 rank가 같은 경우 맨앞글자에서 2만큼 떨어진 위치의 문자를 기준으로 비교를하게된다. 정렬을 진행하면 결과는 다음과 같다.

첫번째 그룹이었던 a가 그룹에서 분리되어 맨 앞으로 가게된다. a의 경우 첫번째 문자에서 2만큼 떨어진 위치가 범위 밖이기때문에 rank를 -1로 계산하여 정렬을 진행했다.
이제 다시 rank를 계산해주는데, 이때 rank는 각 접미사의 맨앞에서 2번째에 위치한 문자를 기준으로 부여한다. 이때 na의 경우 맨앞에서 2번째 문자가 없기때문에 rank를 -1로 간주하고 진행한다.
정렬을 마치고난 뒤에 다시 rank 배열을 초기화시켜준다.

rank 배열의 초기화 과정을 좀 더 면밀하게 살펴보자. 우선 suffix 배열에서 현재 가장 앞에 위치한 접미사의 rank를 0으로 설정해준다.

이제 suffix 배열에서 두번째에 위치한 접미사와, 첫번째에 위치한 접미사를 비교한다. 이때 이전의 rank 값이 같다면, 맨앞에서 t만큼, 즉 지금은 2만큼 떨어진 위치에 있는 문자의 rank를 비교한다.
현재 anana와 a의 이전 rank를 비교했을때, 둘의 rank 값이 0으로 같은것을 볼 수 있다. 따라서 2만큼 떨어진 위치의 문자를 비교하는데, a의 경우 2만큼 떨어진 위치는 범위 밖이므로 rank 값을 -1로 설정하여 비교한다. 따라서 a의 rank 값이 anana의 rank 값보다 작기때문에 둘은 다른 rank를 가져야함을 알 수 있고, anana의 rank 값은 a의 rank 값인 0에 +1을 하여 1이 된것을 볼 수 있다.

이제 접미사 배열에서 다음 위치에 있는 ana를 비교하는데, 이 접미사는 이전의 접미사인 anana와 이전 rank 값과 앞에서 2번째 문자가 모두 같기때문에 anana와 같은 rank 값을 갖게된다.

다음으로 banana를 검사하는데, 이는 이전의 접미사 ana와 이전의 rank 값조차 다르기때문에 ana의 rank보다 1 높은 값을 갖게된다.
위와 같은 과정으로 배열을 초기화시키면 다음과 같은 결과를 얻을 수 있다.

이후 다시 정렬을 하면 결과는 다음과 같다.
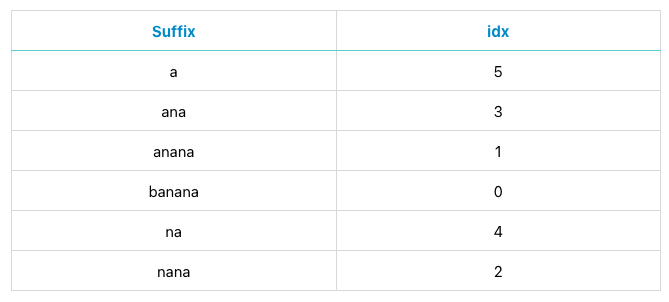
이번에는 앞에서 4번째 문자를 기준으로 rank를 설정한다.

rank 배열에서 가장 큰 값이 문자열의 길이와 같아졌으므로, 더이상 정렬이 진행되지 않는다는 것을 알 수 있다. 따라서 마지막 정렬의 결과가 최종 접미사 배열이 되며, 반복문을 종료한다. 이때 현재 rank 값이 같으면 현재 위치에서 t만큼 떨어진 위치의 문자를 기준으로 비교한다고 했는데, 여기서 t는 1부터 시작해서 2배씩 커진다. 이를 통해 문자열의 길이만큼 정렬을 진행하지않고, 정렬을 진행하는 횟수가 $log n$으로 나타날 수 있다.
맨버-마이어스 알고리즘을 코드로 구현한 결과는 아래와 같다.
def sort_suffixes(text):
n = len(text)
suffixes = []
group = [0] * n
group.append(-1) # 현재 위치에서 t만큼 떨어진 위치가 없는 경우 rank를 -1로 설정
for i in range(n):
suffixes.append(i)
group[i] = ord(text[i]) - ord('a')
t = 1
while t < n:
suffixes.sort(key=lambda x:(group[x], group[min(x+t, n)]))
new_group = [0] * n
new_group.append(-1)
for i in range(1, n):
if group[suffixes[i-1]] != group[suffixes[i]] or group[min(suffixes[i-1]+t, n)] != group[min(suffixes[i]+t, n)]:
# rank가 다르면 서로 다른 rank 값을 갖게함
new_group[suffixes[i]] = new_group[suffixes[i-1]] + 1
else:
# rank가 같은 경우 서로 같은 rank
new_group[suffixes[i]] = new_group[suffixes[i-1]]
group = new_group
if new_group[n-1] == n-1:
break
t *= 2
return suffixes'Algorithm' 카테고리의 다른 글
| [Python] 2022 KAKAO TECH INTERNSHIP 코딩 테스트 공부 (1) | 2023.07.11 |
|---|---|
| [Algorithm] LCP 배열(Longest Common Prefix Array) (1) | 2023.03.28 |
| [Python] 백준 1432번 그래프 수정 (0) | 2023.03.22 |
| [Python] 백준 2573번 빙산 (0) | 2023.03.21 |
| [Algorithm] 위상 정렬(Topology Sort) (1) | 2023.03.21 |
