[자료구조] 트리 순회(Tree Traversal)

이번 알고리즘 문제에 트리 순회 관련 문제가 있어 정확히 트리가 무엇인지, 트리 순회가 무엇인지 알아보고자 포스팅을 하게 되었다. 

 

Graph

트리에 대해 알아보기 전에, 조금 더 넓은 개념인 그래프를 살펴보고 가자. 

그래프는 노드와 노드를 연결하는 간선으로 구성되어 있는 자료구조이며, 정확히는 노드 간의 관계를 간선을 통해 표현할 수 있는 자료구조이다. 

그림으로 보면 다음과 같은 구조를 그래프라고 한다. 

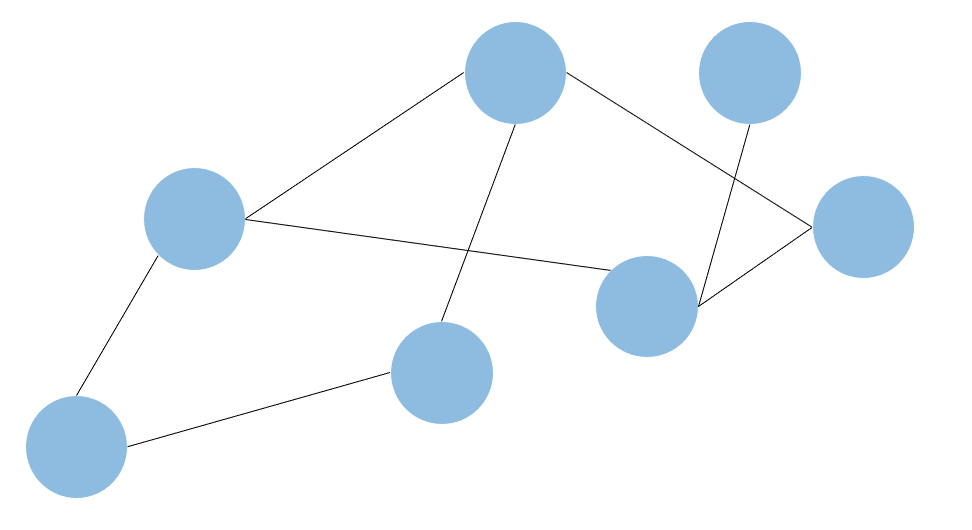
그림을 보면 몇 가지 특징을 알 수 있는데, 정리하자면 다음과 같다.

• 특정 노드에서 어떤 특정 노드로 가는 경로가 하나가 아닐 수도 있다. 
• 계속 같은 경로를 도는 순환이 발생할 수 있다.
• 가장 최상위 노드가 존재하지 않는다. 
• 부모-자식의 관계가 없다.
• 간선의 방향이 있을수도 있고, 없을 수도 있다.

 

Tree

그렇다면 트리는 그래프와 무엇이 다를까? 먼저 그림을 보고 이해를 해보자.

위의 그래프 그림과 비교를 해보면 차이점을 다음과 같이 정리할 수 있다.

• 트리의 경우 같은 경로를 순환하지 않는다. 
• 루트 노드가 존재한다.
• 특정 노드에서 어떤 다른 특정 노드로 가는 경로가 단 하나 존재한다. 
• 부모-자식 간의 관계가 뚜렷하다.
• 노드가 루트 노드로부터 얼마나 떨어져 있는지, 즉 특정 노드의 트리에서의 깊이가 존재한다. 

트리는 맨 위의 노드와 맨 아래 노드가 존재하는데, 여기서 맨 위의 노드를 루트 노드(root node), 더이상 자식이 없는 맨 아래에 있는 노드를 리프 노드(leaf node)라고 부른다.

이번주는 크게 그래프와 트리의 탐색 알고리즘을 배우는데, 이번 포스팅에서는 트리를 중점적으로 다루기 때문에 트리의 탐색 알고리즘에 대한 내용을 위주로 소개한다. 

트리 순회는 자식 노드를 최대 두 개까지 가질 수 있는 이진트리를 기준으로 설명할 것이며, 전위 순회(Preorder Traversal), 중위 순회(Inorder Traversal), 후위 순회(Postorder Traversal)가 있다. 

 

전위 순회(Preorder Traversal)

본격적으로 전위 순회에 대해 알아보기 전에 트리 순회에서 사용하는 기호에 대해 간략하게 알아보고 넘어가자!

이진트리의 순회에서는 세 가지 연산이 존재한다. 각각 V, L, R로 표현하는데 각각에 대한 설명은 다음과 같다.
V(Visit) : 현재 노드를 방문처리 하는 연산
L(Left) : 현재 노드의 왼쪽 자식으로 이동하는 연산
R(Right) : 현재 노드의 오른쪽 자식으로 이동하는 연산

전위 순회는 현재 노드를 먼저 방문 처리를 하고, 자식이 존재하는 경우 왼쪽 자식으로 먼저 내려간 뒤 오른쪽 자식으로 내려가는 순회 방식이다. 

조금 더 정확한 이해를 위해 아래의 그림을 함께 살펴보자! 

모든 트리의 순회는 항상 루트 노드부터 시작한다. 그림에서는 1번 노드가 루트 노드이고, 오른쪽의 스택은 함수의 콜스택을 의미한다. 현재 1번 노드부터 시작하기 때문에 preOrder 함수에 파라미터로 루트 노드의 번호인 1이 전달된 것을 볼 수 있다.

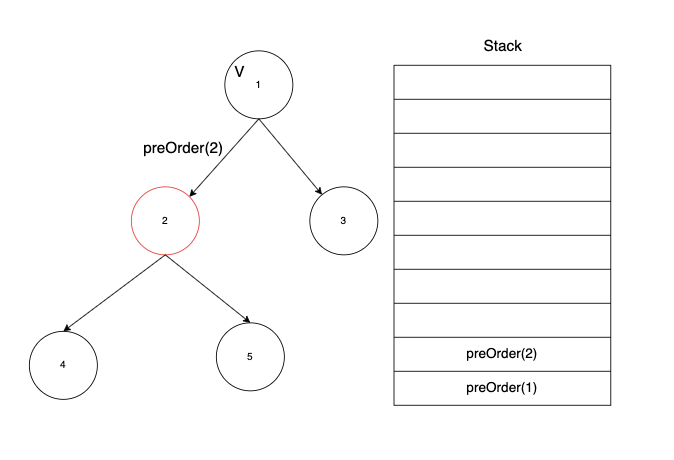
전위 순회에서는 현재 노드를 방문처리 한 뒤 왼쪽으로 내려가기 때문에, 그림과 같이 1번 노드를 방문 처리 하고 왼쪽 노드인 2번 노드로 넘어가게 된다. 

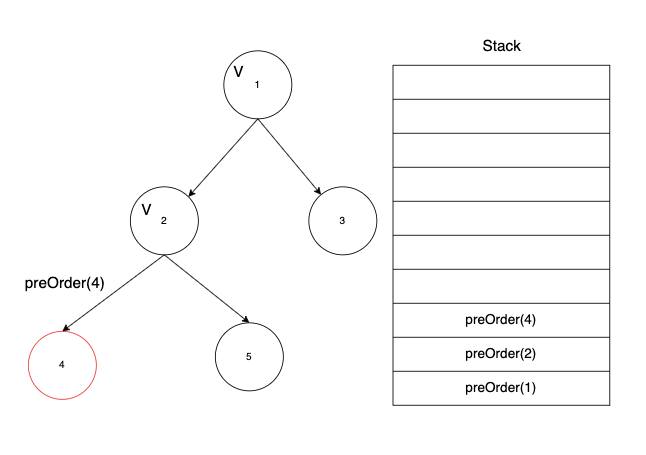
다음으로 2번 노드도 방문 처리를 하고 왼쪽 노드인 4번 노드로 이동한다.

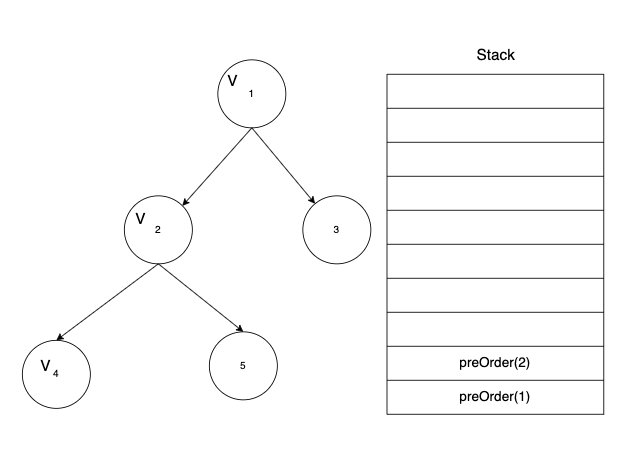
4번 노드의 경우 자식 노드가 존재하지 않기 때문에 함수가 종료되고, 다시 preOrder(2)로 돌아오게 된다. 

preOrder(2)에서는 아직 오른쪽 자식에 대한 순회가 진행되지 않았기 때문에 오른쪽 자식 노드인 5번 노드로 이동하게 된다. 이후는 위에서 서술한 과정을 따라 진행되며, 최종 순회 결과는 다음과 같다.

 

1 -> 2 -> 4 -> 5 -> 3

 

preOrder 함수의 코드는 아래와 같다. 위의 그림에서 설명한 과정을 생각하며 이해해 보자!

# Preorder Traversal

# n은 마지막 노드의 번호
visited = [0] * (n+1)

result = []

def preOrder(node):

    visited[node] = 1
    result.append(node)
    
    if node.left != None:
    	preOrder(node.left)
        
    if node.right != None:
    	preOrder(node.right)

 

중위 순회(Inorder Traversal)

다음으로 중위 순회를 살펴보자. 중위 순회의 표기법은 LVR이며, 현재 노드의 왼쪽 노드를 먼저 순회하고 자신을 방문 처리 한 뒤, 오른쪽 노드를 순회하는 방식이다. 마찬가지로 그림과 함께 이해를 해보자.

 

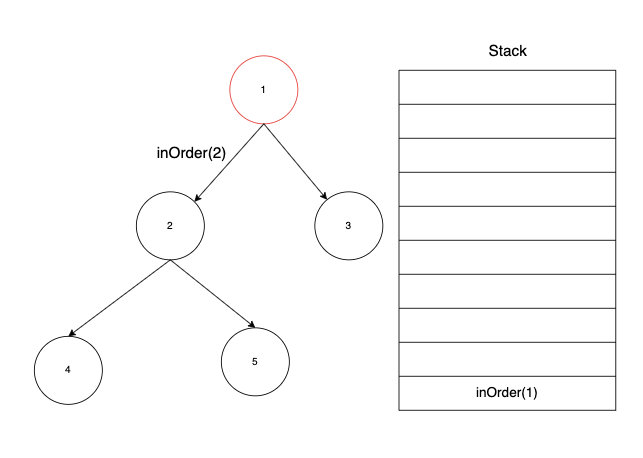
중위 순회 또한 전위 순회와 다르지 않게 루트 노드부터 함수를 시작한다. 단 이번에는 방문 처리를 왼쪽 노드를 순회한 뒤에 하기 때문에, 방문 처리를 하지 않고 바로 왼쪽 노드로 내려간다. 

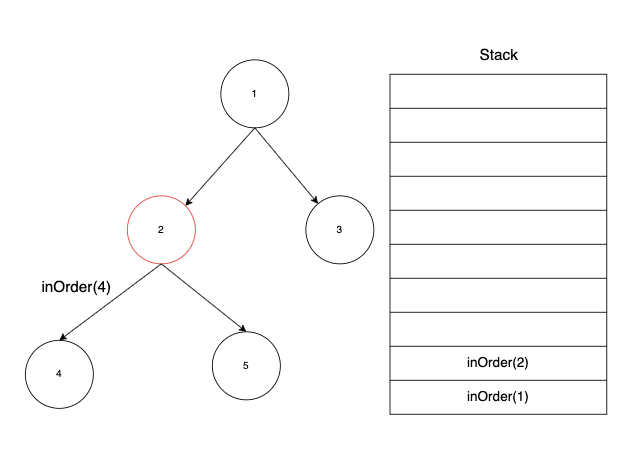
이후 2번 노드에서도 마찬가지로 방문 처리를 하기 전에 4번 노드로 내려간다.

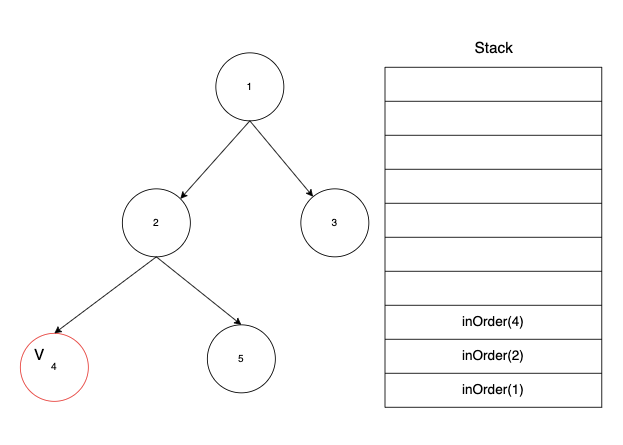
4번 노드는 더 이상 자식이 없는 리프 노드이기 때문에 방문 처리를 해준 뒤 inOrder 함수를 빠져나온다.

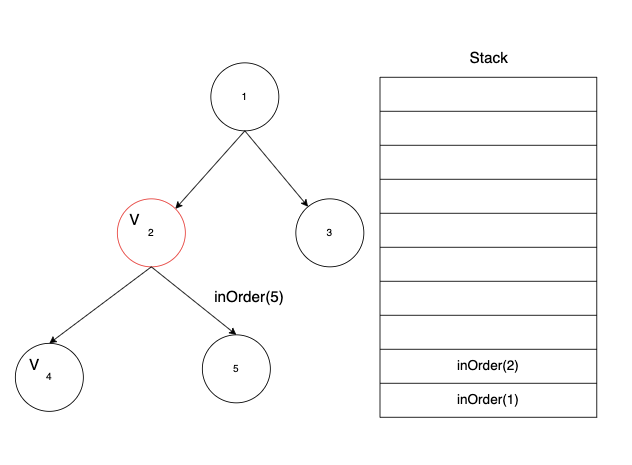
이제 다시 inOrder(2) 함수로 돌아왔는데, 왼쪽 자식의 순회가 끝났으므로 현재 노드를 방문 처리 한 뒤 다시 오른쪽 노드로 내려간다. 

 

이후는 위에서 서술한 방식대로 순회를 진행하며, 순회의 결과는 다음과 같다.

4 -> 2 -> 5 -> 1 -> 3

 

# Inorder Traversal

# n은 마지막 노드의 번호
visited = [0] * (n+1)

result = []

def inOrder(node):

    if node.left != None:
    	inOrder(node.left)
        
    visited[node] = 1
    result.append(node)
    
    if node.right != None:
    	inOrder(node.right)

 

후위 순회(Postorder Traversal)

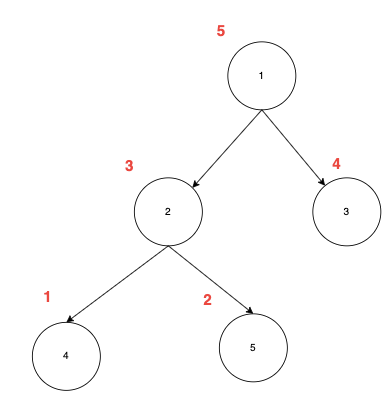
후위 순회는 LRV 순서로 진행되며, 왼쪽과 오른쪽 자식을 모두 순회한 뒤 마지막에 현재 노드를 방문 처리 하는 방식이다. LRV에 대한 설명은 위에서 그림을 통해 충분히 이해했으리라 생각하니 후위 순회는 결과만 확인하고 넘어가자! 

방문 순서는 아래의 그림과 같다.

그림에서 빨간색 숫자가 방문 순서입니다!

# Postorder Traversal

# n은 마지막 노드의 번호
visited = [0] * (n+1)

result = []

def postOrder(node):

    if node.left != None:
    	postOrder(node.left)
        
    if node.right != None:
    	postOrder(node.right)
        
    visited[node] = 1
    result.append(node)

 

트리 순회를 이용하는 문제는 아래와 같다.

https://www.acmicpc.net/problem/1991

1991번: 트리 순회

https://www.acmicpc.net/problem/2263

2263번: 트리의 순회