이번 문제는 원영역 문제이다. N개의 원의 중심 좌표와 원의 반지름이 주어졌을 때, N개의 원들로 나누어지는 영역의 개수를 구하는 문제이다.
처음에는 문제 조건이 너무 복잡해 보였지만, 원의 중심이 모두 일직선 위에 있고, 원들이 겹치는 경우는 없다는 제약이 있었기 때문에 생각보다 어렵지 않게 풀 수 있는 문제였다. 문제 풀이 방식은 철로 문제와 유사하니 풀어보고 오면 좋다!
이 문제 또한 $O(n^2)$의 완전 탐색으로 풀 수 있다. 물론 문제 입력값의 최대 크기가 300,000 이기 때문에 시간제한에 걸리지만...
그래도 문제의 정답을 찾기 위해 어떠한 조건을 만족해야 하는지 알아보기 위해 완전 탐색으로 푸는 경우를 생각해 보자.
먼저 원이 영역을 나누는 방식을 생각해봐야 할 것이다. 문제에서 영역이 나뉘는 방식은 두 가지로 제시를 하였다.
1. 원의 내부와 원의 외부를 구분하는 경우
2. 원의 내부에 작은 원들이 들어있어 내부가 윗부분과 아랫부분으로 나뉘는 경우
1번의 경우 내부와 외부가 구분되는 것이기 때문에, 단순히 구분되는 영역에 +1을 해주면 될 것이다. 이를 통해 원이 아무것도 없는 경우 영역이 1개만 존재한다고 했을 때, 만약 원이 N개가 존재한다면 영역이 최소한 (N+1) 개가 생성될 것임을 알 수 있다.
2번의 경우 1번보다 까다로운데, 먼저 아래의 그림을 보자.

위의 그림에서 가장 큰 원 안에 작은 원들이 빈틈없이 차 있어 가장 큰 원의 내부 영역이 윗부분과 아랫부분으로 나뉘는 것을 볼 수 있다. 이러한 경우 가장 큰 원은 구분하는 영역이 +1이 되는 것이 아니라 내부 또한 두 부분으로 나뉘기 때문에 +2를 해줘야 함을 알 수 있다.
그렇다면 특정 원에 대해서 그 원의 내부에 다른 원들이 존재하는 것을 어떻게 판별할까? 문제에서 주어진 입력은 원의 중심과 반지름 값이기 때문에 우리는 이 값들을 통해 원의 시작 지점의 좌표와 끝 지점의 좌표를 구할 수 있다. 이렇게 원의 시작점과 끝점을 구한 뒤 시작점과 끝점 사이에 중심이 존재하는 모든 원들을 검사하면 될 것이다. 이를 아무런 처리 없이 완전 탐색으로 진행한다면 과정은 다음과 같을 것이다.
1. 검사하려는 특정 원을 선택한다.
2. 원의 시작점과 끝점을 구한다.
3. 현재 원을 제외한 다른 원들을 검사하면서 중심이 현재 원의 내부에 존재하는지 확인한다.
4. 현재 원의 내부에 존재하는 원들에 대해 시작점과 끝점을 검사하면서 현재 원의 내부를 모두 채울 수 있는지 검사한다.
5. 1-4번의 과정을 모든 원에 대해 반복한다.
위의 과정을 그대로 진행하면 시간 복잡도가 $O(N^2)$ 으로 나타날 것이다.
나는 시간을 단축하기 위해 원들의 정보를 (중심, 반지름)에서 (끝점, 지름)으로 바꾸고 정렬을 진행하였다. 이렇게 하면 circles 리스트에는 원의 끝점이 빠른 원이 앞에 올 것이고, 만약 끝점의 좌표가 같다면 지름이 작은 것이 앞에 올 것이다.
이제 모든 원에 대해 원의 내부를 채울 수 있는지 검사를 진행하는데, 이 과정에서 우선순위 큐를 사용하였다. 우선순위 큐에는 끝점이 큰 값이 가장 먼저 오게끔 하였다. 모든 원들을 검사하면서 내부를 채울 수 있는지 확인하는 코드는 다음과 같다.
h = []
cnt = 1
for i in range(n):
end, dist = circles[i]
start = end - dist
can_fill = False
last_point = end
while h:
e, d = heapq.heappop(h)
e = -e
if e <= start:
heapq.heappush(h, (-e, d))
break
if e != last_point and e - d >= start:
continue
if e - d >= start:
last_point = e - d
if last_point == start:
can_fill = True
cnt += 1
if can_fill:
cnt += 1
heapq.heappush(h, (-end, dist))이제 위의 코드를 그림과 함께 살펴보자.
만약 원의 개수가 4이고 각각의 원의 정보가 (7, 5), (-9, 11), (11, 9), (0, 20)인 경우를 생각해 보자.
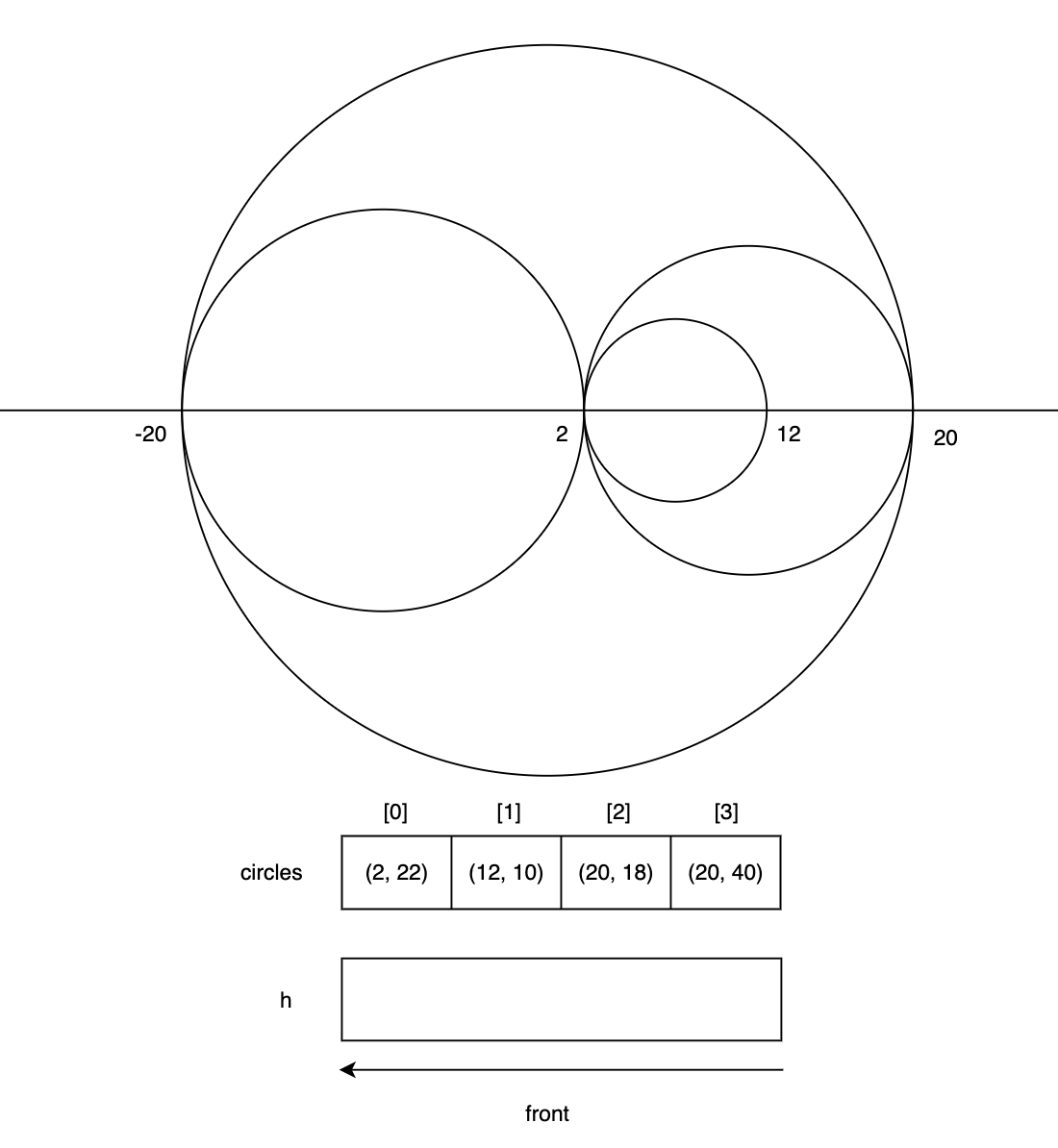
원의 정보를 받아 끝점과 지름의 길이를 구해준 뒤, 끝점을 기준으로 정렬을 진행하면 위의 그림과 같은 결과가 나올 것이다.
코드를 살펴보면 정렬을 진행한 뒤 첫 번째 원부터 마지막 원까지 내부를 채울 수 있는지 검사하는데, 큐에 진입하기 전에 검사하려는 원의 시작점(start)를 구해준다. 또 last_point 라는 변수를 두었는데, 이는 원의 내부를 검사하면서 end 부터 last_point 까지는 이미 원들로 채워져 있다는 것을 의미한다.
먼저 첫번째 원에 대해 검사를 진행해 보자.

첫 번째 원의 경우 큐가 비어있기 때문에 while 문으로 진입하지 않고, 따라서 can_fill 변수는 그대로 False로 남게 되어 내부를 채울 수 없으므로 cnt에 1만 더해준다.

두 번째 원은 큐가 비어있지 않기 때문에 검사를 진행한다. 하지만 큐에 들어있는 원은 현재 원의 외부에 존재하기 때문에 다시 큐에 집어넣고 while 문을 탈출하게 된다. 결과는 위의 그림과 같다.

다음은 세 번째 원이다. 세번째 원은 while 문으로 진입한 뒤, 첫 번째로 나오는 원(파란색)이 현재 원(빨간색)의 내부에 존재하기 때문에 검사를 진행한다. 큐에서 꺼내는 원은 항상 다음 조건을 만족한다.
1. 맨 처음에 배열을 끝점을 기준으로 오름차순 정렬을 해주었기 때문에, 이전에 나왔던 원들은 현재 검사를 진행하는 원보다 왼쪽에 있거나 끝점이 같다(끝점이 같은 경우 지름이 작음).
2. 큐에는 현재 검사하는 원보다 이전에 나온 원들이 삽입된다.
3. 큐는 끝점을 기준으로 내림차순 정렬을 해주었기 때문에, 큐에서 가장 위에 있는 원은 큐에서 가장 오른쪽에 있는 원이다.
4. 따라서 현재 원에 대해 내부가 차있는지 검사할 때, 내부가 완전히 차있으려면 첫번째로 큐에서 꺼내는 원의 끝점은 현재 검사하는 원의 끝점과 같아야 한다.
위의 그림에서 파란색 원은 4번 조건을 만족하지 못하기 때문에 현재 검사하는 원 또한 내부가 완전히 차있지 않음을 알 수 있다. 하지만 파란색 원은 현재 원의 내부에 존재하기 때문에 큐에 다시 삽입하지 않고 버린다.
그 결과는 다음과 같다.

이제 마지막 원에 대해서 검사를 진행해 보자.

위의 그림을 보면 파란색 원의 끝점이 빨간색 원의 끝점과 일치하는 것을 볼 수 있다. 따라서 last_point를 파란색 원의 시작점인 2로 설정해 준 뒤 큐에서 다음 원소를 꺼낸다.

다음 파란색 원 또한 끝점이 last_point인 2와 같기 때문에 last_point를 현재 파란원의 시작점인 -20으로 갱신해 준다.
이후 if 문에서 빨간 원의 시작점이 last_point와 같아졌고, 이를 통해 빨간 원의 내부가 빈틈없이 채워져 있음을 확인하였기 때문에 can_fill을 True로 설정해 준 뒤, 영역을 한 번 더 카운트하며 끝난다.
이러한 방식으로 원들이 나누는 영역의 개수를 셀 수 있다. 전체적인 코드는 다음과 같다.
import sys
import heapq
input = sys.stdin.readline
n = int(input())
circles = []
for _ in range(n):
x, r = map(int, input().split())
end = x + r
dist = 2 * r
circles.append((end, dist))
circles.sort()
h = []
cnt = 1
for i in range(n):
end, dist = circles[i]
start = end - dist
can_fill = False
last_point = end
while h:
e, d = heapq.heappop(h)
e = -e
if e <= start:
heapq.heappush(h, (-e, d))
break
if e != last_point and e - d >= start:
continue
if e - d >= start:
last_point = e - d
if last_point == start:
can_fill = True
cnt += 1
if can_fill:
cnt += 1
heapq.heappush(h, (-end, dist))
print(cnt)'Algorithm' 카테고리의 다른 글
| [Python] 백준 21606번 아침 산책 (1) | 2023.03.18 |
|---|---|
| [Algorithm] BFS & DFS (1) | 2023.03.17 |
| [Python] 백준 2261 가장 가까운 두 점 (4) | 2023.03.14 |
| [Python] 백준 13334번 철로 (2) | 2023.03.14 |
| [Python] 백준 6549번 히스토그램에서 가장 큰 직사각형 (0) | 2023.03.14 |
